16.6 DBSCAN
Another method to consider is Density-based spatial clustering of applications with noise (DBSCAN).
DBSCAN is a powerful, widely used method – great with identifying clusters of arbitrary shape clusters together points that are closely packed together (high density regions), and identifies outliers (not part of any clusters) as points whose neighbors are far away (low-density regions).
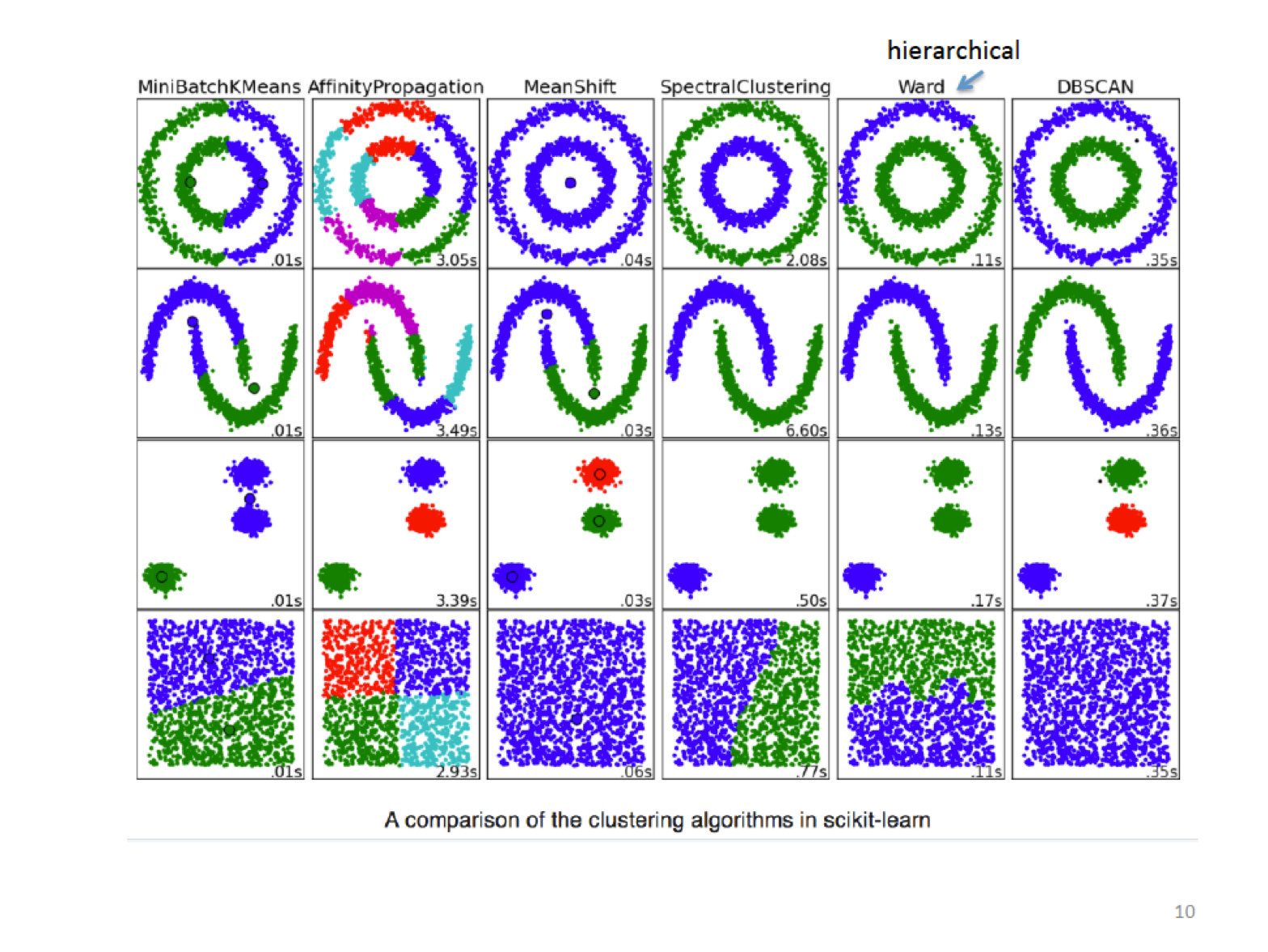
16.6.1 Example of DBSCAN
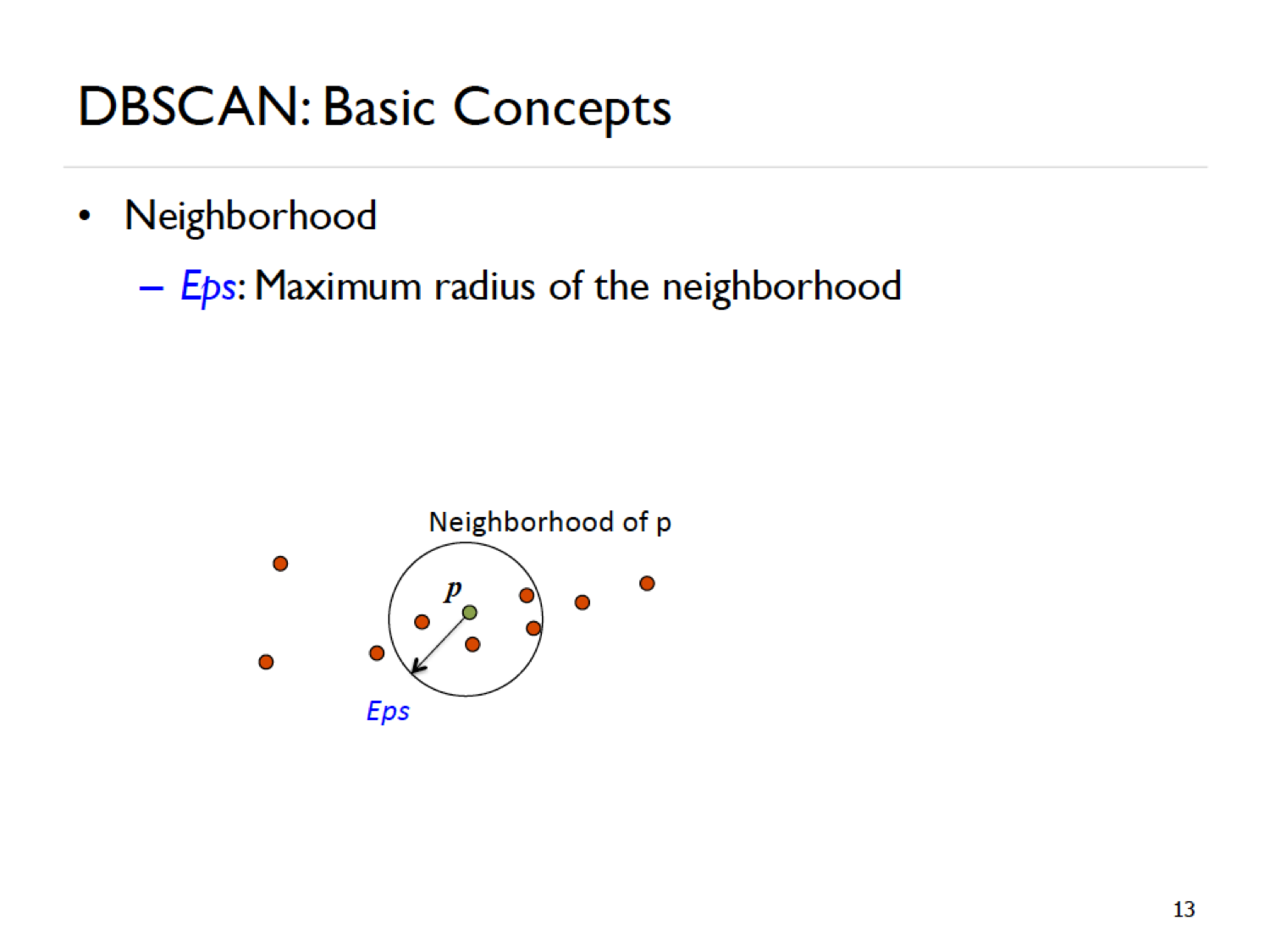
Eps: You have to choose this value. Recommended to be smallish and based on domain knowledge. Eps defines the size and borders of each neighborhood. The Eps (must be bigger than 0) is a radius. The neighborhood of point \(p\) called the Eps-neighborhood of \(p\), is the ball with radius Eps around point \(p\).
MinPts: You have to choose this value. Recommended to be twice the number of dimensions in your dataset.
MinPts is the density threshold. If a neighborhood includes at least MinPts points, it will be considered as a dense region. Alternatively, a point will be considered as dense if there are at least the value of MinPts points in its Eps-neighborhood. These dense points are called core points.
Point \(p\) is a core point because the size of its Eps-neighborhood is 12 and MinPts is 5. Point \(q\), on the other hand, won’t be a core point because its Eps-neighborhood is 4, smaller than MinPts.
A border point has Eps-neighborhood that contains less than MinPts points (so it’s not a core point), but it belongs to the Eps-neighborhood of another core point.
If a point isn’t a core point and isn’t a border point, it’s a noise point or an outlier.
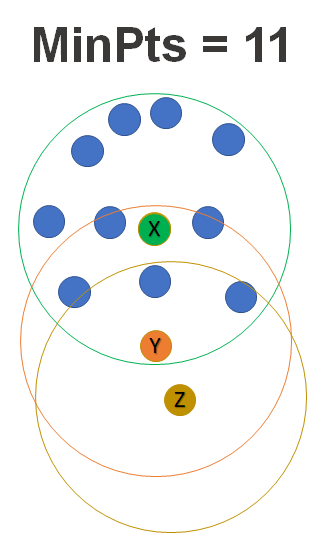
In the figure below we can see that point \(x\) is a core point, because it has more than \(11\) points in its Eps-neighborhood. Point \(y\) isn’t a core point because it has less than \(11\) points in its Eps-neighborhood, but because it belongs to the Eps-neighborhood of point \(x\), and point \(x\) is a core point, point \(y\) is a border point. We can easily see that point \(z\) isn’t a core point. It belongs to the Eps-neighborhood of point \(y\), but point \(y\) isn’t a core point, therefore point \(z\) is a noise point.
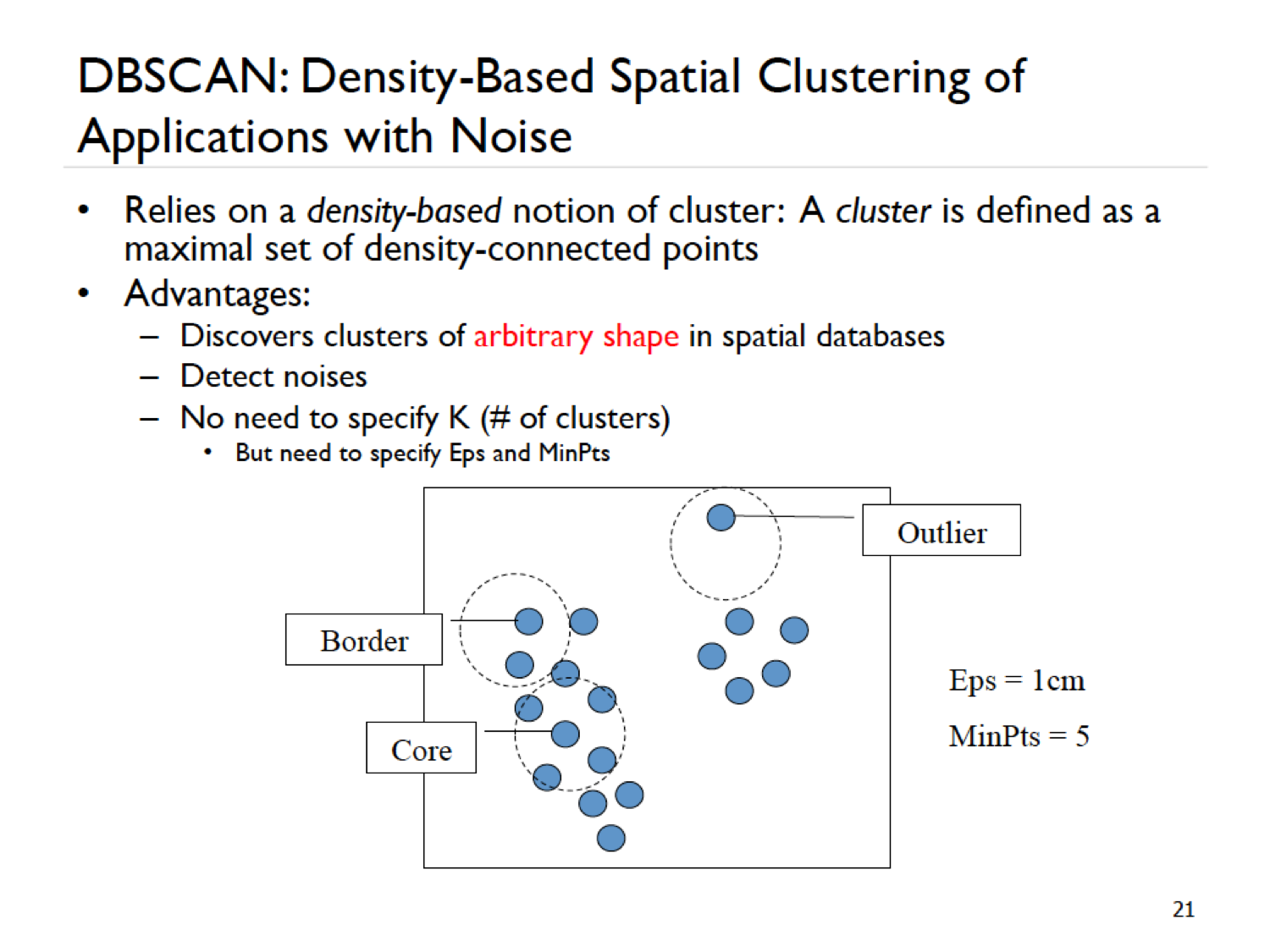Note, the assumption here is that we sampled well, like there are really not a lot of people around the outlier.
A wonderful illustrated description of the DBSCAN algorithm can be found at: https://towardsdatascience.com/a-practical-guide-to-dbscan-method-d4ec5ab2bc99