14.2 Introducing Nonlinear Growth
14.2.1 Types of Nonlinearity
Here, we consider three different types of nonlinearity. These types represent increasing in difficulty so you have to choose a software accordingly.
Type I: Non-linear with respect to time
- examples include \(t^2\), \(log(t)\) included as predictors
- the quadratic growth model is a Type I model
- none of the partial derivatives are dependent on an unknown parameter or random coefficient
Type II: Non-linear with respect to parameters (non-random coefficients)
- random coefficients are additive
- the exponential growth model is a Type II model
- one or more partial derivatives is a function of an estimated parameter
Type III: Non-linear with respect to random coefficients or latent variables
- random coefficients in non-linear functions
- often more difficult to fit in SEM software
- one or more partial derivatives is a function of a random coefficient
14.2.2 Flexibility of Nonlinear Growth
Our goals in growth modeling is often to Understand, estimate, and capture the defining characteristics of “growth” (i.e., change) for a process of interest.
This endeavor is complicated by the multiple potential characteristics of growth, including:
- initial levels
- rates of change
- periods of acceleration and deceleration
- when the process enters and leaves different developmental phases
- the final or asymptotic levels
14.2.3 Utility of Nonlinear Growth
Many applications consider and model linear change patterns because of their simplicity and interpretability.
However, many developmental processes are more complex, several core theoretical notions of development do not posit simple linear change (e.g., Bronfenbrenner, 1979), and many empirical data are not best characterized by linear change patterns.
Researchers must consider models capable of representing nonlinear developmental patterns and be specific about where between-person differences appear in those patterns.
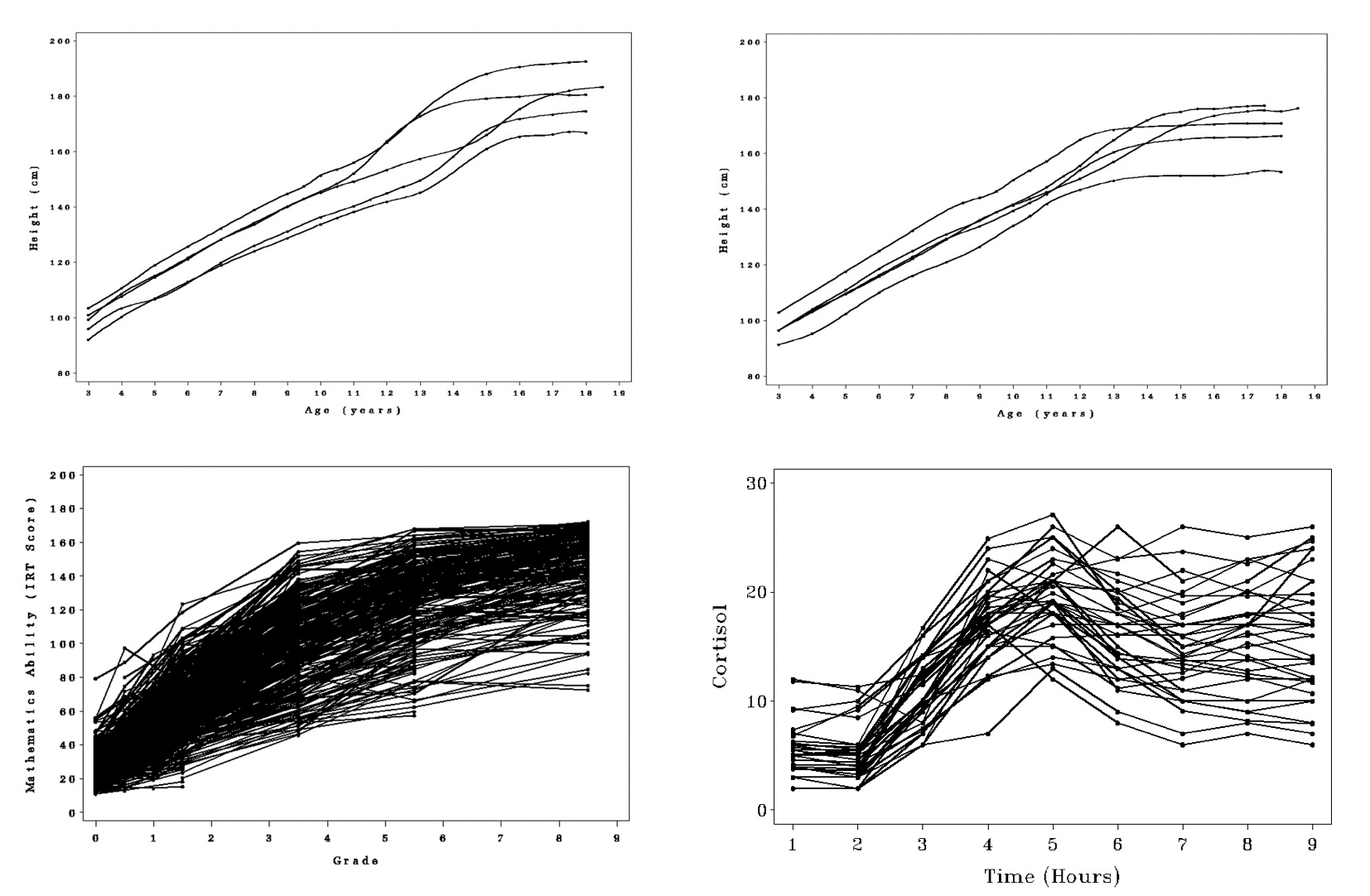
14.2.4 Some Nonlinear Growth Models
Acknowledging the nonlinearity present in many growth processes, consider models that allow for nonlinear change patterns (trajectories), including:
- Polynomial (e.g., quadratic, cubic)
- Latent basis model
- Specific nonlinear functions (e.g., exponential, logistic)
- with and without variation in nonlinear terms
- Multiphase or Spline Models

14.2.5 Need for Nonlinear Models
- Most theoretical or verbals models of change specify relations that do not fall along a straight line
- exponential decay/growth, logistic growth
- Developmental theory often dictates that a relation shifts and/or stops at some point
- changes in context, goals, constraints
- Empirical inquiry (scientific method) suggests useful to reject some forms of nonlinearity
- often a tension between theoretical and empirical fit