9.6 Multiple Predictor Model
Let’s add another variable into the model. Specifically, the variable abuse_rare, which equals \(1\) if the child was rarely abused during early development, and \(0\) if the child experienced abuse.
ferraro2016$abuse_rare <- factor(ferraro2016$abuse_rare)
model2 <- glm(
formula = morbidityw1 ~ 1 + abuse_rare + income_star + abuse_rare:income_star,
family = poisson(link=log),
data = ferraro2016,
na.action = na.exclude
)
summary(model2)##
## Call:
## glm(formula = morbidityw1 ~ 1 + abuse_rare + income_star + abuse_rare:income_star,
## family = poisson(link = log), data = ferraro2016, na.action = na.exclude)
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) 1.0766511 0.0129647 83.045 < 2e-16 ***
## abuse_rare1 -0.2382614 0.0251265 -9.482 < 2e-16 ***
## income_star -0.0311089 0.0091684 -3.393 0.000691 ***
## abuse_rare1:income_star -0.0000822 0.0179350 -0.005 0.996343
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for poisson family taken to be 1)
##
## Null deviance: 8068.4 on 2966 degrees of freedom
## Residual deviance: 7956.7 on 2963 degrees of freedom
## (55 observations deleted due to missingness)
## AIC: 14737
##
## Number of Fisher Scoring iterations: 5As the model becomes more complicated it can be helpful to write out the equation,
\[ \mathrm{log}(morbidity_i) = b_0 + b_1(abuse\_rare_{i})+ b_2(income^{*}_{1i})+ b_3(income^{*}_{1i})(abuse\_rare_{i}) \]
Again, when we have a dummy variable interaction we have essentially set up two different equations:
Equation for Children Experiencing Maltreatment
Coefficients \(b_0\) and \(b_2\) describe the relation between \(income^{*}_{1i}\) and \(morbidity_i\) for those who experienced childhood abuse \((abuse\_rare_{i}=0)\).
\[ \mathrm{log}(morbidity_i) = b_0 + b_2(income^{*}_{1i}) \]
Equation for Children Rarely Experiencing Maltreatment
\[ \mathrm{log}(morbidity_i) = (b_0 + b_1) + (b_2 + b_3)income^{*}_{1i} \]
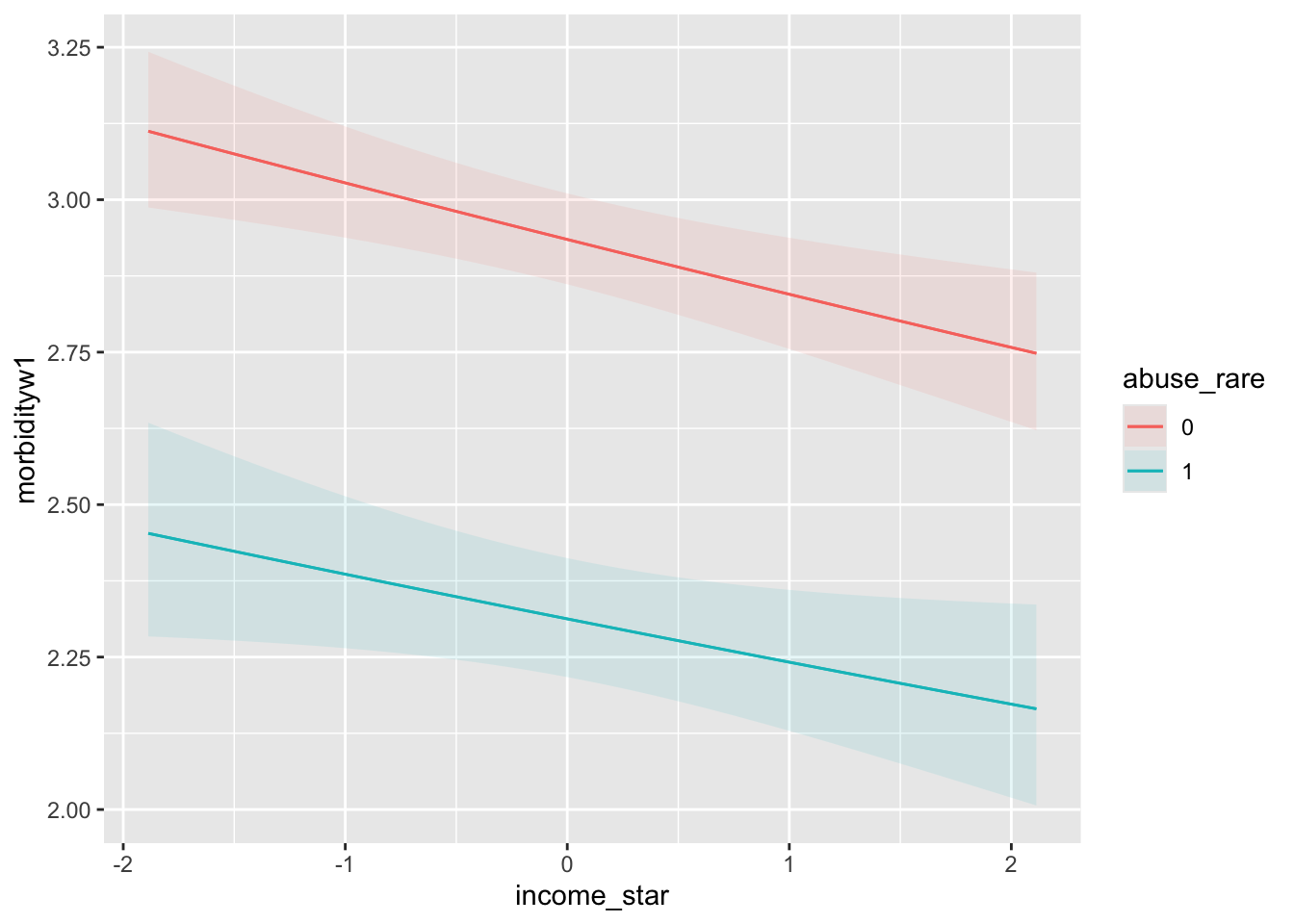
While coefficients \(b_0 + b_1\) and \(b_2 + b_3\) describe the relation for those who rarely experienced childhood abuse \((abuse\_rare_{i}=1)\). Note that \(b_3\) is not significantly different from zero, so we would not interpret the interaction between income and abuse directly.
Marginal Effects
Let’s again turn to the marginaleffects (Arel-Bundock 2022) package to look at the marginal effects of income and childhood abuse on health.
marginaleffects::plot_predictions(model2, condition = c("income_star","abuse_rare"), conf.int = TRUE)