15.5 Actor Partner Interdependence Model (APIM)
While some models are appropriate for independent or predictor variables that vary either only between dyads or only within dyads, here we focus on the case of mixed predictor variables.
Mixed predictor variables can vary both between and within dyads. This means mixed variables can
- vary on average from dyad to dyad, and
- vary from person to person within a dyad.
The between-dyad variation is characterized by variation in the dyad means, \(M_j\), and the within-dyads variation is characterized by variation in the deviations of each individual’s score from their dyad mean, \(X_{ij}-M_{j}\).
15.5.1 Model
As an example, consider the effects of depression on father-son relationships. It may be that a father’s depression influences their own relationship satisfaction, while also influencing the relationship satisfaction of their son. These two types of effects can be disentangled as:
- actor effect: the effect of a fathers’s depression on their own relationship satisfaction
- partner effect: the effect of a fathers’s depression on their son’s relationship satisfaction
So, an actor effect occurs when one dyad member’s score on a predictor variable affects that same member’s score on thr outcome variable.
A partner effect occurs when a dyad member’s score on a predictor variable affects their partner’s score on an outcome variable.
Below is a graphical depiction of the APIM model.
- Two dyad members measured on two variables, \(X\) and \(Y\)
- \(X_{1}\) is the \(X\) (predictor) score for dyad member 1
- \(X_{2}\) is the \(X\) (predictor) score for dyad member 2
- \(Y_{1}\) is the \(Y\) (outcome) score for dyad member 1
- \(Y_{2}\) is the \(Y\) (outcome) score for dyad member 2
- \(a\) denotes the actor effects
- \(p\) denotes the partner effects
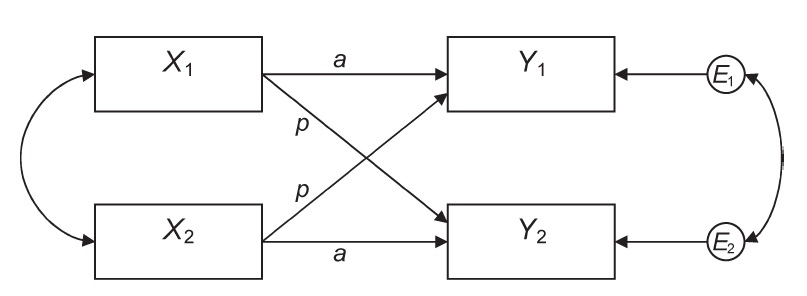
Note, there are two correlations visible in this path diagram.
- the two \(X\) variables are allowed to correlate
- this may be due to compositional effects
- the equation errors are correlated
- this represents the covariation in \(Y\) not explained by the APIM
- are there systematic ways \(X\) does not account for \(Y\) within-dyad?
15.5.2 Conceptual Interpretations
Following Kenny and Cook (1999), four models are highlighted here as having important implications for relationships research:
- Actor-oriented: \(a ≠ 0, p = 0\)
- Partner-oriented: \(a = 0, p ≠ 0\)
- Couple-oriented: \(a = p\)
- Social comparison: \(a + p = 0\)
15.5.2.1 Actor-Oriented
In the actor-oriented model, a person’s outcomes are a function of their own characteristics, and they are unaffected by their partner’s characteristics.
If the estimated partner effects are shown to be equal to zero, \(p=0\), we might conclude that a process is individualistic.

15.5.2.2 Partner-Oriented
In the partner-oriented model we have a situation where a person’s outcome is solely affected by their partner’s characteristics. If the estimated actor effects are shown to be equal to zero, \(a=0\), we might conclude that a process follows a partner-oriented model.
One example discussed by Kenny, Kashy & Cook (2006), for which there could be partner effects, but not actor effects, is the effect of physical attractiveness on relationship satisfaction.

15.5.2.3 Couple-Oriented
In the couple-oriented model the actor and partner effects are equal,\(a = p\). This means that a given dyad member is affected as much by their own score on \(X\) as they are by their partner’s score on \(X\).
This pattern may occur if the dyad members are as concerned with their own outcomes as they are with their partner’s outcome.
For example, playing one’s best in couple’s trivia could lead one to be satisfied with the outcome of the contest. At the same time, knowing one’s partner played their best could also lead to satisfaction. On the other hand, if one’s partner has a bad game, one’s own satisfaction may be less, independent of how one played. Such dynamics might give rise to a couple-oriented model.

15.5.3 Actor-Partner Interactions
Many of the major research question in dyadic analyses involve actor–partner interactions.
Thus, for dyads, the actor-by-partner interaction term would be the product of \(X_{1}\) and \(X_2\).
For example, consider two individuals in a relationship. Suppose being an introvert makes you a better listener, but this effect is stronger the more introverted your partner is. This would be an example of an actor-by-partner interaction.
However, it should be noted there are many ways to conceptualize an interaction. Dyadic researchers often conceive of interactions in novel and interesting ways. For example,
- absolute difference between \(X_{1}\) and \(X_{2}\)
- an example might include personality differences
- the max or min of the dyad member’s scores
- an example might be compensation effects
Although interaction effects can be specified in many different ways it is often difficult to distinguish between them statistically. Many of these interaction terms are highly correlated with one another. This makes it very important to have a strong theoretical argument for one approach over another.
15.5.2.4 Social-Comparison
In the social comparison model the actor and partner effects are relatively equal in their absolute magnitude but have opposite signs. Typically the actor effect is positive, and the partner effect is negative.
In contrast to the couple-oriented case, in which the partner’s success is valued as much as one’s own outcome, the social comparison orientation typically involves dissatisfaction with the partner’s success.
For example, consider a parent child trivia team. The parent might be couple oriented, feeling satisfaction with both the child and parent playing well. On the other hand, the child may not be couple oriented, feeling less satisfied the better the parent plays.
For the child the actor effect (playing well) would be a positive predictor of game satisfaction while the partner effect (parent playing well) would be a negative predictor. This is one example of how a social-comparison model may arise, \(a + p = 0\).