4.1 Types of matrices
Remember that matrices are defined by rows (the first dimension) and columns (the second dimension):
\[ \underset{m \times n}{\mathbf{A}} = \begin{bmatrix} a_{11} & a_{12} & a_{13} \\ a_{21} & a_{22} & a_{23} \\ a_{31} & a_{32} & a_{33} \\ a_{41} & a_{42} & a_{43} \end{bmatrix} \]
You can refer to a specific element in matrix using a subscript of the row and column index (e.g. \(a_{31}\)). For our purposes there are a few special matrices worth mentioning,
4.1.1 Square
A square matrix has the same number of rows and columns. Covariance and correlation matrices are square.
\[ \underset{n \times n}{\mathbf{A}} = \begin{bmatrix} a_{11} & a_{12} & a_{13} & a_{14} \\ a_{21} & a_{22} & a_{23} & a_{24} \\ a_{31} & a_{32} & a_{33} & a_{34} \\ a_{41} & a_{42} & a_{43} & a_{44} \end{bmatrix} \]
4.1.2 Symmetric
A symmetric matrix is a square matrix that equals its transpose. This means that corresponding entries on either side of the main diagonal are equal.
\[ \begin{align} \underset{n \times n}{\mathbf{A}} &= \begin{bmatrix} a & ab & ac & ad \\ ab & b & bc & bd \\ ac & bc & c & cd \\ ad & bd & cd & d \end{bmatrix} \\ \cr \mathbf{A} &= \mathbf{A}' \end{align} \]
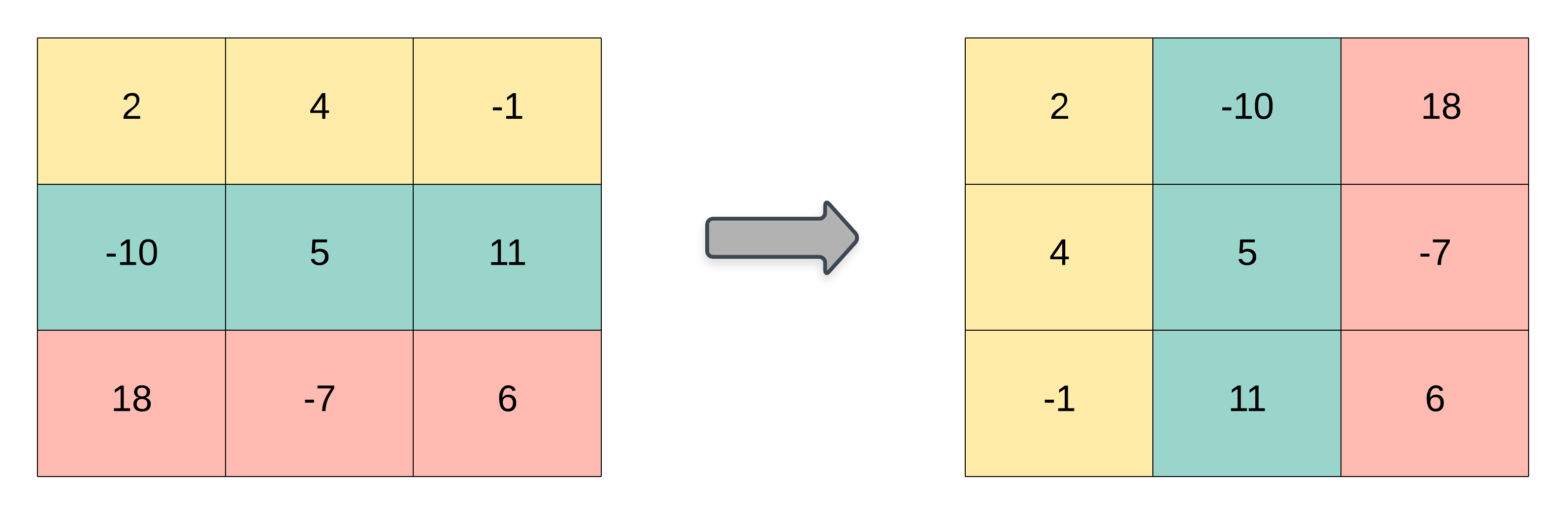
Matrix Transpose
The transpose of a matrix is an operator which flips a matrix over its diagonal. That is, it switches the row and column indices of the matrix \(A\) by producing another matrix, often denoted by \(A'\) (or \(A^{T}\)).
Graphical Depiction of a Matrix Transpose
4.1.3 Diagonal
A diagonal matrix is a special case of a square symmetric matrix in which there are values along the diagonal, but zeros elsewhere:
\[ \begin{align} \underset{n \times n}{\mathbf{A}} &= \begin{bmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & 0 \\ 0 & 0 & 0 & d \end{bmatrix} \\ \cr \mathbf{A} &= \mathbf{A}' \end{align} \]
4.1.4 Identity
An identity matrix is a special case of a diagonal matrix in which the elements of the diagonal are all 1:
\[ \underset{n \times n}{\mathbf{I}} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \]
Any matrix multiplied by an identity matrix is unchanged.