13.6 Quadratic Growth Model

Quadratic time model (MLM): random intercepts and linear and quadratic slopes.

Quadratic Growth Model

verblong$gradeSquared <- (verblong$grade)^2

fq_rq_fit <- lme(
  fixed = verb ~ 1 + grade + gradeSquared, 
  random = ~ 1 + grade|id + gradeSquared|id, 
  data=verblong,
  na.action = na.exclude,
  method = "ML"
)
summary(fq_rq_fit)

## Linear mixed-effects model fit by maximum likelihood
##   Data: verblong 
##        AIC      BIC    logLik
##   5226.412 5259.343 -2606.206
## 
## Random effects:
##  Formula: ~1 + grade | id + gradeSquared | id
##  Structure: General positive-definite, Log-Cholesky parametrization
##                                   StdDev   Corr  
## (Intercept)                       5.277258 (Intr)
## 1 + grade | id + gradeSquaredTRUE 5.277258 -0.288
## Residual                          4.491283       
## 
## Fixed effects:  verb ~ 1 + grade + gradeSquared 
##                  Value Std.Error  DF   t-value p-value
## (Intercept)  16.347780 0.7508427 610 21.772576  0.0000
## grade         3.695700 0.4344000 610  8.507596  0.0000
## gradeSquared  0.138997 0.0606470 610  2.291899  0.0223
##  Correlation: 
##              (Intr) grade 
## grade        -0.750       
## gradeSquared  0.695 -0.982
## 
## Standardized Within-Group Residuals:
##         Min          Q1         Med          Q3         Max 
## -2.79052272 -0.55253516 -0.02974189  0.51054065  4.07582660 
## 
## Number of Observations: 816
## Number of Groups: 204

Let’s look at the predicted trajectories.

verblong$pred_fq_rq <- predict(fq_rq_fit)
verblong$resid_fq_rq <- residuals(fq_rq_fit)

fun_fq_rq <- function(x) {
  fixef(fq_rq_fit)[[1]] + fixef(fq_rq_fit)[[2]]*x + fixef(fq_rq_fit)[[3]]*x^2
}

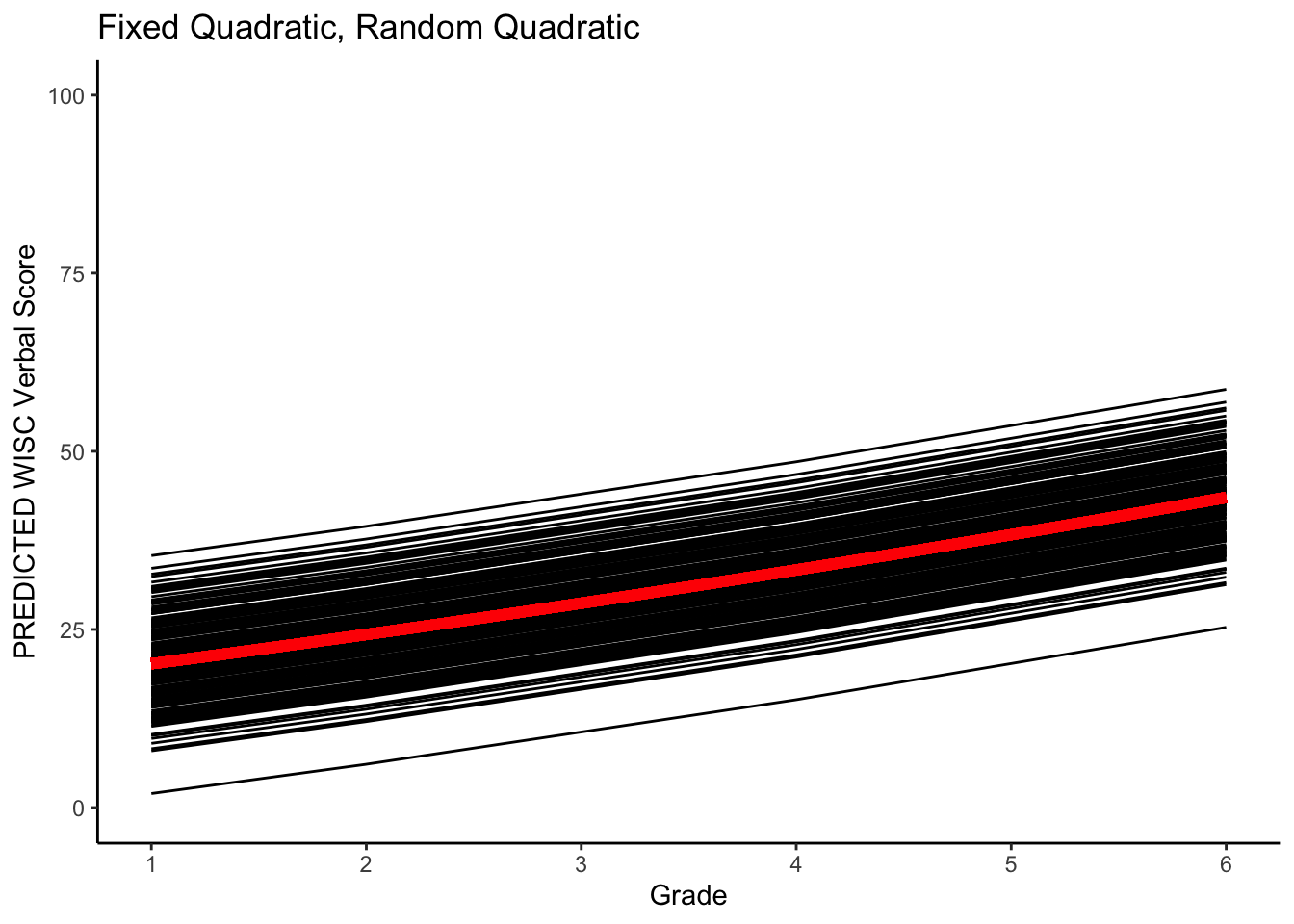
ggplot(data = verblong, aes(x = grade, y = pred_fq_rq, group = id)) +
  ggtitle("Fixed Quadratic, Random Quadratic") +
  geom_line() +
  xlab("Grade") + 
  ylab("PREDICTED WISC Verbal Score") + ylim(0,100) +
  scale_x_continuous(breaks=seq(1,6,by=1)) + 
  stat_function(fun=fun_fq_rq, color="red", size = 2) +
  theme_classic()

## Warning: Multiple drawing groups in `geom_function()`
## ℹ Did you use the correct group, colour, or fill aesthetics?