11.8 Lord’s Paradox
Consider the summary of Lord’s Paradox from Wikipedia
The most famous formulation of Lord’s paradox comes from his 1967 paper:
“A large university is interested in investigating the effects on the students of the diet provided in the university dining halls and any sex differences in these effects. > Various types of data are gathered. In particular, the weight of each student at the time of his arrival in September and his weight the following June are recorded.” (Lord > 1967, p. 304)
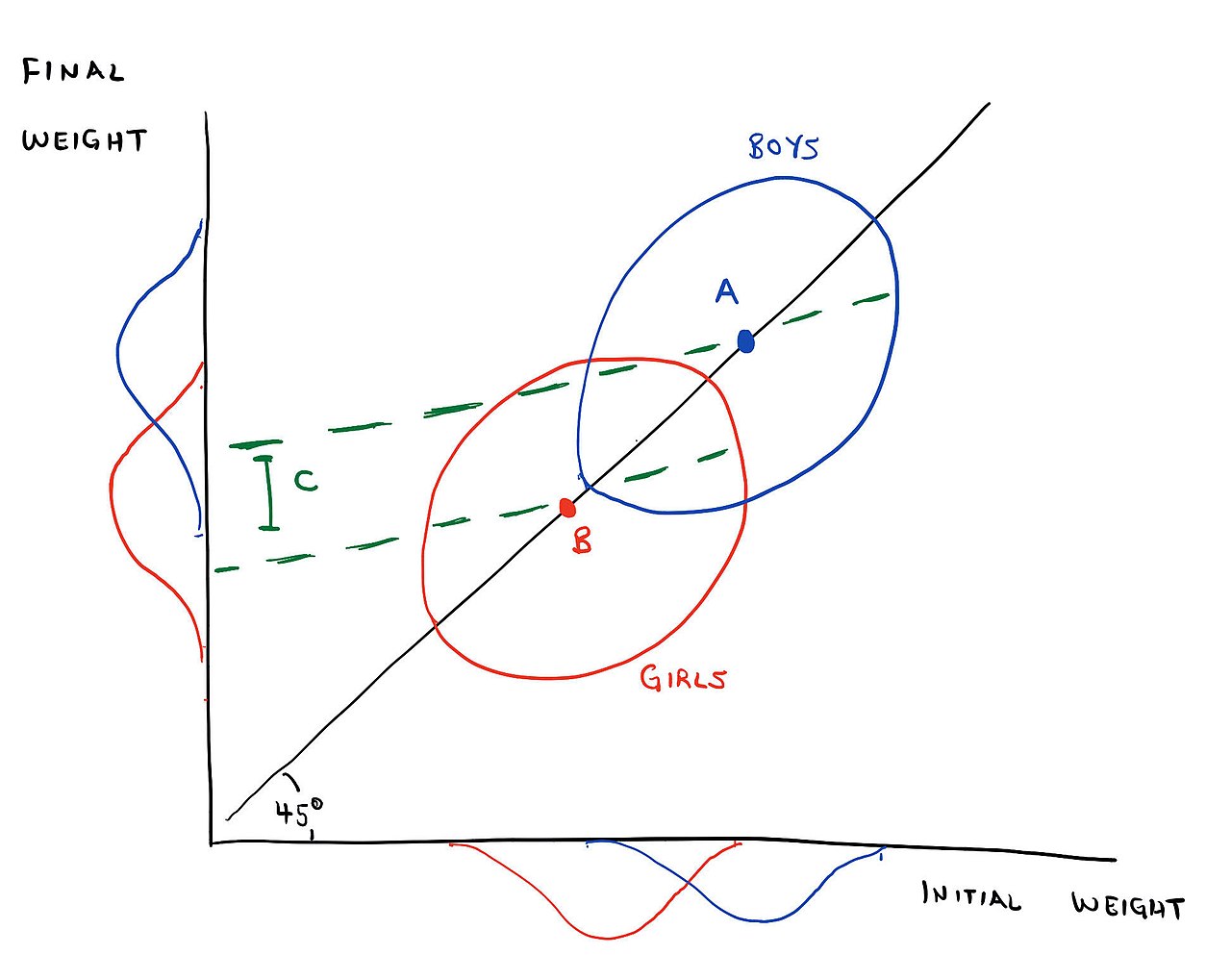
In both September and June, the overall distribution of male weights is the same, although individuals’ weights have changed, and likewise for the distribution of female weights.
Lord imagines two statisticians who use different common statistical methods but reach opposite conclusions.
One statistician uses difference scores and finds no significant difference between genders:
“[A]s far as these data are concerned, there is no evidence of any interesting effect of diet (or of anything else) on student weights. In particular, there is no evidence of any differential effect on the two sexes, since neither group shows any systematic change.” (pg. 305) Visually, the first statistician sees that neither group mean (‘A’ and ‘B’) has changed, and concludes that the new diet had no causal impact.
The second statistician uses the ANCOVA (residualized change) model. They find a significant difference between the two sexes. Visually, the second statistician fits a regression model (green dotted lines), finds that the intercept differs for boys vs girls, and concludes that the new diet had a larger impact for males.
Lord concluded: “there simply is no logical or statistical procedure that can be counted on to make proper allowance for uncontrolled preexisting differences between groups.”