11.3 Two-Occassions of Change
Although we may prefer to have more timepoints, two waves of data is
- often what is available or affordable,
- often directly related to a change of interest, e.g., pretest-posttest
- an improvement over cross-sectional data for many questions of interest
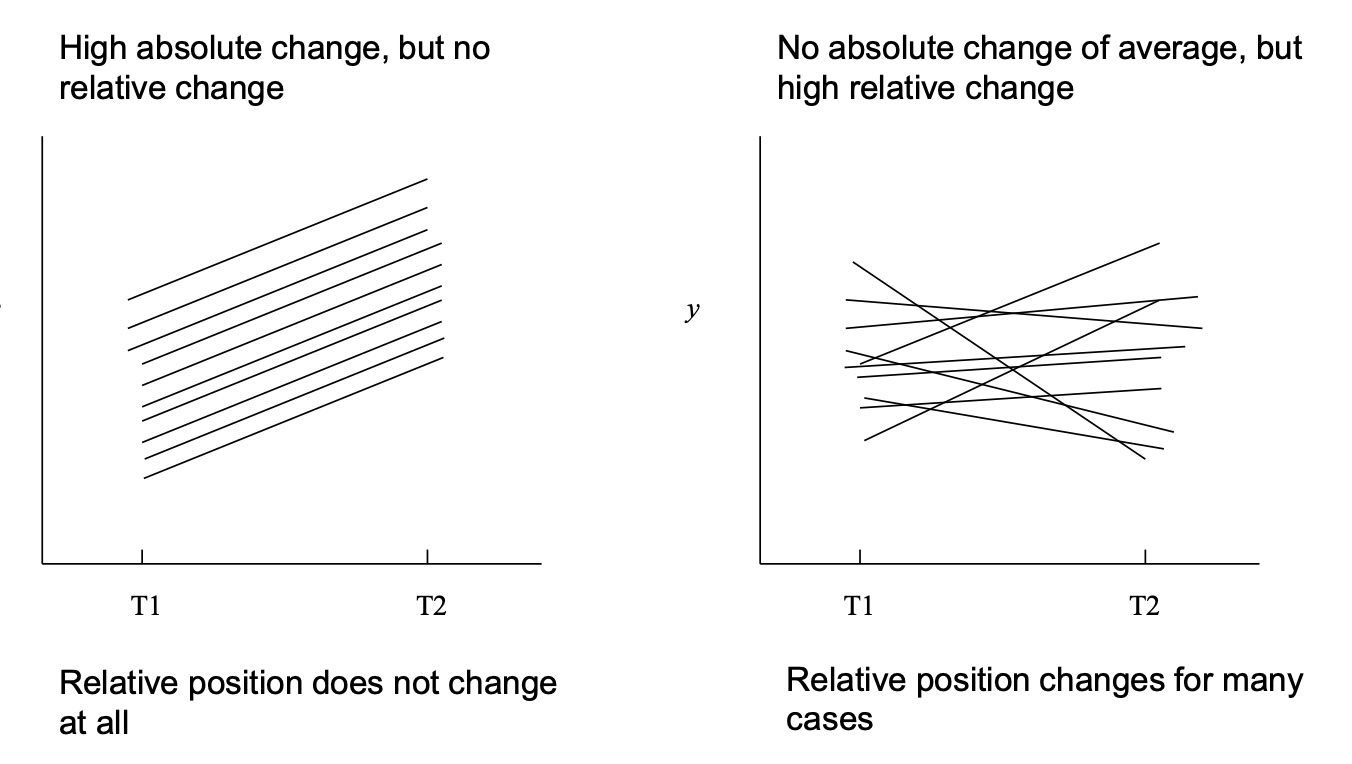
Notions of Stability
Stability in the Absolute or Exact Sense
A variable may be considered stable to the extent that
- mean values for \(y_{1}\) and \(y_{2}\) are equal over time (\(\bar{y}_{2}-\bar{y}_{1}=0\), \(y_{2i}-y_{1i}=0\))
- individual values of \(y_{1i}\) and \(y_{2i}\) are equal over time (\(y_{2i}-y_{1i}=0\))
Stability in the Relative Sense
A variable may be considered stable to the extent that
- \(y_{1i}\) and \(y_{2i}\) are correlated (\(r_{12}=1\))
Note that mean or individual values may increase or decrease over time, but correlation will be largely unchanged unless relative position changes.
Notions of Change
Raw Change
In thinking about difference scores (change scores, gain scores) we are often interested in the absolute change in the value of \(y_{t}\).
Difference scores captures increase or decrease in the mean values or individual values.
Correlation between \(y_{1}\) and \(y_{2}\) can be anywhere between \(0\) or \(1\) and difference scores may be small or large.
For example. if \(r_{12} = 1.0\) and we add \(5\) points to \(y_2\), \(r_{12}\) will still be equl to \(1.0\) but the mean difference will have changed.
y1 <- c(1,1,1,2,2,2)
y2 <- c(3,3,3,4,4,4)
# cor(y1,y2) = 1
# mean(y2-y1) = 2
y2 <- y2 + 5
# cor(y1,y2) = 1
# mean(y2-y1) = 7Relative Change
When we think about relative change, a lower correlation indicates greater change, but change is relative to other cases in the data and not absolute.
For example, if \(r_{12}=0.45\), and we add \(5\) points to all scores, \(r_{12}\) will still be \(0.45\). Even though the scores themselves will all change, the relative degree of change is unaffected.
Compare Absolute and Relative Change